Monday, January 29, 2007
Eternity is Back! Win $2 Million Starting This Summer!
The puzzle consists of 256 square pieces with different patterns on their sides which must match when the squares are aligned to each other. The only solution to the puzzle is now in a London bank vault. Eternity II has been developed by the original inventor, Lord Christopher Monckton, a former aide to Margaret Thatcher.
Two smaller "Clue" puzzles (72 and 36 pieces respectively) accompany the main one. Just like with the original Eternity they are developed to help solvers discover locations of key pieces.
The original Eternity has been solved in 18 months. With Eternity II solvers will have time until December 31, 2008 to submit their entries, which will be date-stamped and then analyzed. The first correct puzzle to be sent in will be the winner! How fast a solver should be this time to overcome Eternity?
Friday, January 26, 2007
Sudoku Puzzle
Sudoku is actually a logical placement puzzle that tests your reasoning powers along with your patience to see through the end of the game. This riveting puzzle game usually consists a 9x9 grid, further divided into 3x3 subgrids. Some of the cells are supplied with numbers and your aim is to fill up the rest of the cells so that each column, row, and region holds the numbers 1 - 9 exactly once. That is, “single numbers”, as indicated by the name of the puzzle.
But contrary to popular perception, Sudoku puzzles are not mathematical games. The numerals can be substituted by any set of distinctive symbols, say alphabets, shapes or colors. And ESPN’s version of Sudoku has the positions of the baseball field in place of numbers.
The name Sudoku is an abbreviation of the Japanese phrase, "Suuji wa dokushin ni kagiru", which means, “the digits must remain single". This name has been patented by the Nikoli Co. Ltd. in Japan, a renowned publisher of puzzles. Sudoku is also known as Number Place, which is the original U.S. title, or "Nampure" for short.
Sudoku has an interesting lineage. It is believed that an early version of the puzzle, which came out in a French newspaper in 1895, was actually inspired by the Latin Squares, an immensely popular puzzle devised by the great mathematician Euler. From its inception in print till the First World War, Sudoku has been a popular weekly feature in the newspapers.
The modern form of Sudoku owes its origins to Howard Garns, an architect who also dabbled in puzzle making. Retaining the basic form of Euler’s Latin Squares, Garns added a third dimension (the regional restriction) and presented the puzzle as a partially completed grid. It came out under the title Number Place in the puzzle magazine Dell Pencil Puzzles and Word Games.
The recent surge in the popularity of the Sudoku puzzles has a Japanese connection. Always on the lookout for some food for thought, the people of Japan went all out for Sudoku around 1986, two years after Nikoli introduced the puzzle in Japan in the paper Monthly Nikolist. The world followed suit and by 2005, Sudoku became one of the most popular puzzles ever played.
These days, the Internet is replete with websites containing free Sudoku puzzles. These online puzzles also come in printable versions for you to download and solve it while waiting for the bus. Quite a few newspapers also carry Sudoku puzzles as weekly or even daily features.
And once you have exhausted these vast resources, you have Sudoku software to create a puzzle for you in a jiffy, thus ensuring that your gray cells are never idle.
The Sudoku puzzle has definitely taken over the world by storm.
Thursday, January 25, 2007
How To Play the Hanukkah Game of Dreidel
Difficulty: Easy
Time Required: 20-40 minutes
Here's How:
1. All players get an equal amount of pennies, chocolate coins (gelt), candies, raisins, or tokens.
2. All players put one token in the pot in the center.
3. The dreidel is a four sided spinning top with a different Hebrew letter on each side. Players take turns spinning the dreidel.
4. The player acts according to the letter which is facing up when the dreidel stops spinning.
5. The image with the Hebrew letters on the top right of this page is the game key; it shows which Hebrew letter symbolizes which move in the game. Nun means the player does nothing. Gimel means the player takes all the tokens from the pot. Hay means the player takes half of the tokens from the pot. Shin (or Pay in Israel) means the player puts one token into the pot.
6. The winner is the one with the most tokens.
Tuesday, January 23, 2007
Online Games - Types Of Popular Games
Action and adventure Games: The games which come in this genre are the ones, which involve fighting games, space adventure games, situational games where the player is required to achieve some objectives, etc. Most of the games in this genre are rich in animation and may also come with a story line.
Arcade Games: Gaming arcades earlier used to be the place in the neighborhood, where gaming machines were installed. To play a game, one must put some coins into the machine. Online arcade games are just another term.
Board Games: These are some of the most popular games. Board games played online are the same, which we play in our real life. They are animated versions of traditional and favorite board games.
Card Games: These need no explanation. Card games are ever popular with the gaming population. There are a lot of games designed with playing cards.
Casino Games: Now again, these are fairly addictive. They simulate the games available in real casinos. When you play with virtual money, there is nothing to lose. So you get a lot of people playing online casino games. You may believe it or not, but a lot of online casino games may even involve real money transactions.
Strategy Games: These are the games, which take considerable time to play and complete. The player has to apply his mind totally to devise strategies to play and win. Some people may not like strategy games, but others like these. These games may take some time to master.
Sports Games: People like to play sports games on the Internet. One does not need much time to understand sports games, if one already understands the real sport. One can have many levels of play. And there may be the option of competing against a second player or the computer itself.
Shooting Games: These are great stress busters. People can play these games and let out their anger on shooting enemies and objects in virtual games. There can be a lot of variety in shooting games. These can also be included in the action and adventure genre of games, but are kept separate due to their popularity.
Puzzle Games: These games are again very popular for people who don't like too much action or violence. These can actually help you sharpen your mind. Puzzle games are loved by all ages. In fact there is no age group for puzzle games.
A Short History on Sudoku
In Japan there is a Publishing House called Nikoli who publish the countries leading puzzle publication “Monthly Nikolist” and it was members of the staff that noticed there was an interesting number puzzle game called “The Number Place” being published in the American version of their puzzle magazine called “Dell Puzzle Magazines”. So in April 1984 Sudoku as it is known in Japan and across the world made its debut in the “Monthly Nikolist”, although it was originally known as “Suunji wa dokushin ni kagiru” by Kaji Maki the president of the company at the time. Although the maiden issue of Sudoku enjoyed some modest success, its success is really down to the fact that the Japanese people are puzzle crazy.
It was only after a couple of significant changes had happened which resulted in the puzzles popularity taking off. Firstly the name was changed to Sudoku (which is a lot easier to remember) then Nikoli Publishing House introduced 2 new rules for the game in 1986. These were that the numbers were to be arranged symmetrically and the given numbers could not exceed 30. Today you will find that there are at least 5 publishing companies now producing a monthly magazine which is solely devoted to this game in Japan. As for the name Sudoku it is rather a brand name instead of being a generic one and it has been legally registered by the Nikoli Company in Japan. Because of this any other company producing versions of this game must provide their own names for their versions.
Other stories that are doing the rounds concerning who created Sudoku are various; one being that it was created by a team of puzzle creators in New York. Then the other story also doing the rounds is that a retired architect and puzzle enthusiast by the Howard Gerns invented the game. Yet although these stories conflict because they credit its invention by different people, they do in fact agree on two points.
Firstly that Sudoku was first published in 1979 by Dell Puzzle Magazines with the title “The Number Place”.
Secondly that both Gerns and the puzzle creators from New York were inspired to produce their own versions by the game called “Latin Square” of Leonhard Euler. Leonhard Euler was a Swiss mathematician who presented a paper called “De Quadratis Magicis” at the St Petersburg Academy in 1776. He demonstrated that a magic square can be created by using 9, 16, 25 or 36 cells (blocks). However there were conditions that he imposed on the value of the number variables which brought about the creation of his magic square, this then evolved into Latin Squares on later papers that he presented.
But the versions of Gerns and team puzzler’s games differed from Euler’s in 2 ways. The first being that Euler’s version does not have any regional restrictions and secondly that Euler did not create or intend to create a puzzle. But it was the fact that Gerns and the team from New York saw the potential of a hit puzzle being produced from Euler’s work and thus proceeded to create what would be the grandfather version of modern day Sudoku.
In 1997 a retired judge based in Hong Kong called Wayne Gould happened to see a Sudoku puzzle in a Tokyo bookstore and he decided to produce a digital version of the puzzle, which he worked on from 1997 until 2003. Then in 2004 he found himself presenting this unknown puzzle to The Times newspaper in UK and within a few days of it appearing in The Times other newspapers had begun to print their own versions. In fact it became so popular that versions of it were soon to be found in Australia and New Zealand, and by 2005 it had become known as the fastest growing puzzle game throughout the world. Soon after American Newspapers were hearing about this fast growing puzzle and by April 2005 the New York Post was publishing it own version of the game also. Which is quite strange really as it originated from New York some 20 years previously?
Because it is a number puzzle and therefore does not require the use of any letters from any particular language, there is no language barrier. The game is now published in many different publications around the world from magazines to newspapers to books solely dedicated to this highly popular puzzle. You will even find websites that now offer digital versions of the game for either a fee or for free and this will certainly guarantee the games continued success in the future. It also makes it more accessible to the younger population. The race is even on for companies to create a Sudoku puzzle which is specifically designed for mobile phone users.
Sudoku is a logic puzzle which challenges old and young alike and in studies carried out it has been found that those who play Sudoku regularly have increased mental skills.
Free Online Games - Solving Puzzles Can Sharpen The Mind
Online puzzle games benefits- every puzzle that we solve needs application of mind. No puzzle can be solved without concentrating the mind on the problem. Ultimately puzzles lead the student improve his/her logical and analytical ability. Subjects such as operations research need these qualities in abundance. Higher mathematic involves lot of game playing. Those games are different, but once your mind sharpens solving online puzzles, you can proceed to higher levels of games in mathematics that can help solve many problems.
We have been solving puzzles since ages. The only difference now is that one need not search for a book or a magazine to look for puzzles. One can get them online for free. Puzzles that involve alphabets, and numbers are a fantastic method to sharpen the ability of children in thinking. Please encourage your children solve puzzles. By depriving them that, you may drive them to something bad. Better to give them the satisfaction of solving online puzzles and sharpening their mind. Sit down with them and make the selection with them. After that give them the freedom to play and solve puzzles. You will find out the results yourself after sometime.
Awesome Free Baby Shower Games: Crossword Puzzle, Word Search and Word Scramble
One of the reasons that games are so useful at a baby shower is they are great small time fillers. For example you want filler for that awkward time between the first guest arriving and the rest of the guests arriving. Often one or two of the guests that come early have to sit around and twiddle there thumbs and if they don’t already know each other this can be really painful to watch and crash your party before it ever gets started. Elementary school teachers know that to keep people paying attention you need some quick activity to draw them in and get them involved. You also want some games at your disposal that are just in case have an extra few minute types of games. You don't want to expend a ton of effort or money on these extra games but boy are they handy if the food arrives late or there is some other catastrophe that needs to be taken care of. Simply hand the guests one of these pre-made activities and then you can be free to take care of whatever might arise.
Well, the cheapest, easiest and quickest way to get some fun extra free baby shower games is to look online. Yet we are not advocating you look for free baby shower games. Instead take a little time and do some searching around for a puzzle maker. Teachers use these all the time in the classroom to generate a crossword or word search with the new vocabulary for the lesson they just taught. It makes great homework and good time filler also. So look online for a crossword creator or a word search maker. Discover Channel has a great free puzzle maker for teachers that can also be used for making baby shower games.
Once you have found the puzzle generator it is pretty easy to simply plug in the word that fit with the baby shower. Part of the fun of these is to personalize the words and make them relevant to the baby shower. So things like the Mother and Fathers name. The baby's due date or possible name. Then you can also use some generic baby things like bottle, rattle, formula, crib and so on. The more specific and personalized you can be the better. This can also serve as somewhat of an ice breaker activity. As the guests fill out the crossword puzzle or word search they learn more about the parents to be.
Now that you have generated a crossword puzzle and have you words in you can easily go in and create other activities using the puzzle creator. Next you will want to add some finishing touches and spice things up a bit. You can do this by copying the crossword puzzle or word search and then pasting it into your text editor like word and etc. Then add a few little piece of clip art to really add a final touch.
Then you will want to either print a copy for every guest or have it copied at a local copy or office supply shop. You can keep these in a folder ready to go and then just pull them out when you need them.
Top 5 Sony PSP Puzzle Games
5. Me and My Katamari. Despite the general wierdness of the Katamari Damacy series, Me and My Katamari is just plain fun. The controls are a bit difficult to get use to at first, and the gameplay is very repetitive (what puzzle game isn't?), but your fingers with play to the tune of Katamari after a couple hours on this game.
4. WTF. A very simple game comparible to Wario Ware. You start out with four different mini games, beat them endlessly, and unlock endless new games. Why is it so fun, because its mindless and easy, it has a twisted mundane sort of humor and there isn't another game like it on the PSP.
3. Exit: What can I say, its freaking awesome and it has levels you can download too. I'm more towards the puzzle games beecause my girlfriend can play too. This one was challenging and fun.
2. Lumines. A launch game, luckily it didn't launch with the PSP or I would not have bought any game. If you have a PSP and don't have this game, then you owe it to yourself to get the best game for the PSP. Virtually flawless.
1. Lumines II. If the first Lumines made the list, the second one had to also. There is no way about it, Lumines is the best puzzle experience the PSP has to offer. I would go as far as to say that it is one of the best puzzle games ever EVER.
Some Of The Reasons That Online Puzzle Games Are So Much Fun
My brother and I would make a contest of it, while my sister would calmly find the pieces and fit them into the puzzle. She always completed more of the puzzle than we did, but that didn't stop us from proclaiming that we had done the most to complete the puzzle.
Now, instead of buying puzzles at the store, I put them together online. I have to tell you, of all the advanced technology out there, the ones that have been put into puzzle games amaze me the most. These are interactive puzzles that allow you to drag the pieces around the screen to form it. It may sound boring, but nothing could be farther from the truth.
My favorite game site, Big Fish Games, has puzzles that come to life as they take shape. There's one particular game that uses the ocean as a background. You start putting the puzzle together and as the fish shapes are completed, they take on life and begin moving about the screen. Way too cool, as my son would say. Somehow, they've managed to give the puzzles a 3D effect, which makes them even more beautiful when they are completed. The details are so fine, that you feel like you are actually in the room shown in the puzzle.
Another of my favorite puzzles blends objects into the picture and you have to find them all in a certain amount of time. Some of the objects are easy to locate, but others are so well hidden, it's hard to locate them. You can get hints to their location and I am always shocked that I didn't see them earlier, since they appear to have been "hidden" in plain view. These games are excellent to sharpen your observation skills and provide exercise for your mind. Body fitness is given tons of attention, but little is given to how to keep your mind in shape. Puzzle games are a great way to do this and provide a lot of entertainment at the same time.
If you really want to get on a mental treadmill, try the games that make you find the differences in pictures. It might seem easy, but it isn't. This weekend my sister is coming for dinner and I'm going to introduce her to these games. Finally, after all of these years, I think I may actually best her at a puzzle.
Kids' Puzzle Games
Kids can either play these games individually or with help of adults or other kids. Proper care should be taken in choosing kids' puzzle games suitable for their abilities and ages. Toddlers are comfortable with three- to four-piece wooden puzzles, whereas two-year olds enjoy piece-fitting puzzles. The number of pieces in puzzles keeps increasing with age, while the size of the pieces are typically larger for younger kids. School-age kids can work on complex fifty- to one-hundred-piece games. Kids' puzzle games may include nursery rhymes or scenes from storybooks. These puzzles can also be used for formal learning, as they provide a useful means to the teachers to assess a child's development in terms of speech, movement, and concentration. Damaged puzzles or puzzles with missing pieces should be weeded out as they invariably frustrate the child.
Kids' puzzle games can also be created at home by mounting pictures on cardboard and cutting them into large pieces. Kids can use scissors to cut pictures from magazines and devise their own puzzle games.
Some of the popular kids' puzzle games are alphabet and number puzzles, world map puzzles, travel floor puzzles, basic jigsaw puzzles, slide puzzles, and maps of the USA floor puzzles. Kids' puzzle games provide a perfect mix of fun and education for kids.
Building Vista buzz with a puzzle
The ad, which appeared on December 21, was comprised of a small black box with a long numerical and alphabetical code and was surrounded by the words, "Most of you won't figure this out," as well as a URL.
This was the beginning of Vanishing Point, the newest large-scale project from 42 Entertainment, the firm behind popular alternate-reality games such as I Love Bees, The Beast and Last Call Poker.
Vanishing Point is a hybrid game--part alternate-reality game, or ARG, part traditional sweepstakes--that's actually a marketing vehicle for Microsoft's Windows Vista. As a lure, Microsoft is giving away a $220,000 suborbital flight on a four-seat plane that can reach altitudes of up to 330,000 feet and that provides several minutes of weightlessness. Neither 42 Entertainment executives nor Microsoft would say how much the software giant is paying 42 to create and manage the contest.
There appears to be significant buzz surrounding Vanishing Point and its ambitious series of scheduled events in cities around the world. The first occurred January 8 at Las Vegas' Bellagio resort, during the giant Consumer Electronics Show, when organizers projected a lengthy puzzle-filled video onto the mist from the venue's famous fountains. The game is expected to conclude before Vista's January 30 consumer launch.
Despite that opening splash during CES, however, some question whether anyone will remember the link between the game and Vista.
"I'm not much interested in who's putting on the contest, as long as I have a chance to win," said Jonathan Waite, a senior editor at ARGNet, an online news and community site devoted to ARGs. "The next big question is will (people) buy Vista because they enjoyed Vanishing Point? I don't think there's going to be a big swing in Vista sales because of (the) game."
While it's difficult for game developers to measure a hard return on their investment in time and money, creating buzz may well be enough for them.
"It's definitely a lot less expensive than people have assumed," said Brian Marr, Microsoft's group marketing manager for Windows Vista. "I don't know what a Super Bowl ad costs (last year's ads reportedly cost $2.6 million for a 30-second spot). You get a month's worth of entertainment for the same price."
Unlike previous 42 Entertainment projects, Vanishing Point is not a pure ARG. According to Elan Lee, 42's vice president of design, it's quite different structurally from an ARG, but it does have some of the elements of that genre.
Pieces Of The 9/11 Puzzle
But it was only after the September 11 attacks that authorities realized just how dangerous Khalid was. He turned out to be Khalid al-Mihdar, one of five hijackers who would perish in the attack on the Pentagon. And what no one knew back in early 2000 was that al-Mihdar was in the United States when he called the house in Yemen. The content of some of his conversations, in fact, was reported to the FBI at the time, but neither the FBI nor the NSA investigated much further, officials now say.
The failure to discover al-Mihdar's presence in America--and perhaps stumble upon the hijacking plot--has emerged as one of the most glaring intelligence lapses preceding the 9/11 attacks. It is also now a central focus of the independent 9/11 commission, which plans to address the larger problem in the handoff of information from the NSA to the FBI in an upcoming public hearing. "This was very damaging," says Eleanor Hill, who directed Congress's earlier probe into 9/11. "The intelligence community was not sufficiently focused on the threat to the United States."
Surprisingly, government agencies often did not--or could not--trace the location of all calls made to and from targeted sites, even such high-value ones as the Yemeni house. The failure to follow up on al-Mihdar's calls to Yemen was discussed in oblique and heavily redacted passages in the joint congressional inquiry released last July, which described communications involving "a suspected terrorist facility in the Middle East." U.S. News has learned that the "facility" was the Yemeni safehouse, which authorities describe as one of the most important sources of hard intelligence about al Qaeda before 9/11. The home belonged to Sameer Mohammed Ahmed al-Hada, an al Qaeda facilitator who was also al-Mihdar's brother-in-law. The FBI obtained al-Hada's phone number from a suspect in the twin 1998 bombings of U.S. embassies in Africa.
Over the next three years, sources say, NSA eavesdroppers mined intelligence that helped authorities foil a series of terrorist plots, including planned attacks on the U.S. Embassy in Paris and the U.S. Consulate in Istanbul, along with an attempted airline hijacking in Africa. The home also served as a planning center for the 2000 attack on the USS Cole in Yemen. Al-Hada was killed two years later when a hand grenade he was carrying exploded as he was being chased by Yemeni police.
Waging war. The matter remains shrouded in secrecy, reflecting broader concerns by authorities over revealing details of America's most sensitive intelligence gathering techniques. How the nation's eavesdroppers work and what they listen to are rarely discussed publicly, but the two 9/11 probes have thrown rare light on the inner workings of U.S. intelligence. The failure to detect al-Mihdar's presence in America, for example, reveals another flaw in America's counterterrorism efforts before 9/11: The intelligence community lacked a coordinated program to monitor contact by people in the United States with suspected terrorists overseas. "We were waging a war," says a counterterrorism official, "and nobody knew it, including the troops."
Despite the conventional wisdom that America's intelligence agencies closely monitor international calls to and from the United States, the NSA was exceedingly leery of eavesdropping by accident on what it calls "U.S. persons," who include American citizens and others inside the United States. NSA analysts have had the authority to listen to calls involving U.S. persons if they come into contact with suspected terrorists overseas, but they are not allowed to specifically target Americans. The FBI is also authorized to monitor and trace calls between people in the United States and abroad, but the congressional 9/11 inquiry faulted both agencies for failing to coordinate and plug holes in the coverage. "It was NSA policy to avoid as much as it could any coverage of individuals in the United States," says Hill. "That would have been fine as long as we ensured that the FBI was following up on those areas."
Hill's inquiry found that neither the NSA nor the FBI took full advantage of provisions of the Foreign Intelligence Surveillance Act that would have helped them target such communications--including the targeting of individuals rather than simply individual telephone numbers. Aggressive use of this technique, the inquiry concluded, might have detected al-Mihdar and others earlier. U.S. officials, however, defend their procedures. "If we became aware they were calling for pizza in the United States, we would have called the FBI," insists one of the Bush administration's most senior intelligence officials. "We didn't know."
Still, the episode exposes surprising limitations in America's oft-touted global eavesdropping ability. At the heart of the effort stands the NSA, which controls a massive array of satellites, listening devices, and supercomputers that capture all kinds of foreign electronic signals from telephone calls to missile telemetry. In reality, the NSA is drowning in information, and every day is a constant struggle to process and make sense of the enormous volume of calls it intercepts, intelligence experts say. In many cases, NSA analysts start off with only the identity of a person on one end of the phone call. Sometimes, intercepts pick up only fragments of a conversation.
In the case of the calls to and from the house in Yemen, there were technological limits to what U.S. eavesdroppers could pick up. "Neither the contents of the calls nor the physics of the intercepts allowed us to determine that one end of the calls was in the United States," says the senior intelligence official. It was only after 9/11, prompted by the congressional inquiry, that the FBI delved into toll records and found the U.S. origin of al-Mihdar's calls. In other words, it would have taken initiative on the part of the FBI or other agencies to trace some of the hundreds of phone calls in and out of a target site like the Yemeni house. "NSA did not think it was its job to initiate this research on its own," according to a staff statement by the current 9/11 commission. "It tends to wait to be asked."
The FBI was overwhelmed, as well, and many good leads were simply overlooked as agents tried to cope with the stacks of NSA reports they routinely received. Veteran agents also point out that the Yemen safehouse was one of numerous facilities U.S. intelligence agencies were monitoring. "The amount of data was overwhelming," says Sheila Horan, a former senior official in the FBI's national security division. "When you have a limited number of analysts and agents, you can't possibly cover all those intercepts."
Officials at the FBI and NSA say they have improved their coordination. Changes in national security laws and procedures have given authorities much more latitude to share information and track potential terrorists inside the United States. In particular, Bush administration officials credit the controversial Patriot Act for easing restrictions on how intelligence and law enforcement agencies share information. "Since September 11, the integration and exchange of intelligence on persons who would do Americans harm, whether it be domestically or overseas, has been augmented dramatically," FBI Director Robert Mueller said in a meeting with U.S. News reporters last week.
But looking back, the missed opportunities surrounding one hijacker in particular are sobering. Al-Mihdar's U.S. calls are only one point in a series of events that could have led U.S. officials to the 9/11 conspiracy. A Saudi then in his mid-20s, al-Mihdar first appeared on U.S. radar in late 1999, when the NSA analyzed calls tied to a suspected al Qaeda associate named Khalid. From eavesdropping on the Yemen safehouse, officials had learned of a now infamous meeting in Kuala Lumpur in January 2000, where planning for the 9/11 attack took place. Al-Mihdar was surveilled as he attended the meeting, along with a handful of other al Qaeda operatives, including another future hijacker, Nawaf al-Hazmi. But the CIA failed to get the two men placed on government watch lists, and they entered the United States within days, settling in San Diego. There is one more quirk of fate pointed out by the congressional inquiry. If intelligence on al-Mihdar had made its way from the CIA, NSA, or FBI headquarters to the FBI's San Diego field office, agents say they would have almost certainly started an investigation. They wouldn't have had to look far: One of the field office's longtime informants had had repeated contacts with al-Mihdar.
But, unwatched by U.S. authorities, al-Mihdar left for the Middle East later that year. He returned in 2001, just as America was celebrating its Inde-pendence Day. Two months later, he and four others boarded American Airlines Flight 77 and plunged it into the Pentagon.
An enormous theorem: the classification of finite simple groups
It should have been a landmark for modern mathematics, but it failed to attract much attention in the wider media, and even within the subject many people were sceptical. The reason was the mysterious and controversial nature of its proof. At over 10,000 pages, spread across 500 or so journal articles, by over 100 different authors from around the world, it was without precedent, and must be counted the longest in history.
The sceptics were proved right, up to a point: problems with the proof were subsequently discovered. The biggest took Michael Aschbacher and Stephen Smith seven years and two further books of work to resolve. In 2004, after this had been accomplished, Aschbacher wrote "to my knowledge the main theorem [of our paper] closes the last gap in the original proof, so (for the moment) the classification theorem can be regarded as a theorem".
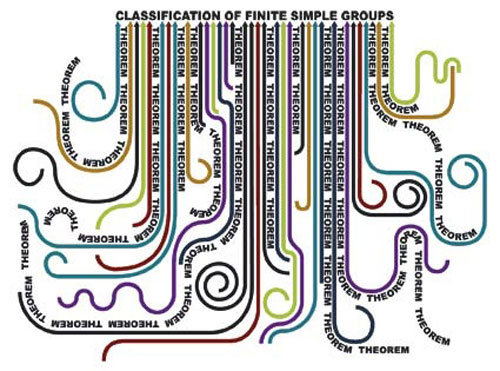
Pulling together the strands of mathematics.
For such a ground-breaking piece of contemporary mathematics, it's amazing that no-one in the world today completely understands the whole proof. The person with the best overall perspective on it was Gorenstein, who died in 1992. Gorenstein acted as coach to the team-effort to prove the enormous theorem. It was he, at a series of seminars in Chicago in 1972, who outlined the bold idea of taking various disparate strands of research which had emerged since the 1950s, and turning them into a concerted classification program.
So what is this astounding theorem, that requires a proof of such colossal length and complexity? What are "finite simple groups", and what does it mean to "classify" them? In this article I'll try to shed a little light on these questions, but first we'll need to take a few steps back.
Abstraction: precision and power

A cube has six faces, each is a square.
Mathematics often proceeds from the specific to the general. We start with an interesting object, for instance a cube. There are many observations you could make about a cube, but a mathematician might focus on its composition: it's a 3-dimensional solid, with flat 2-dimensional faces which meet at straight edges and vertices (corners). Such an object is called a polyhedron. You might then notice that a cube is a rather special polyhedron: all the faces have the same shape, all the edges have the same length, and the same number meet at every vertex. Polyhedra like this are called regular polyhedra.
So starting from a cube, we have discovered a more general type of object, a regular polyhedron, of which our cube is now just an example. Another example is a tetrahedron, which has four triangular faces.
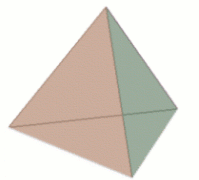
A tetrahedon has four faces, each is an equilateral triangle.
This movement from the specific — the cube — to the general — the idea of a regular polyhedron — is the process of abstraction. Abstraction is central to mathematical thinking; without it there would be no maths. There are two reasons for its importance.
The first is precision: if you're working on a question about a class of mathematical objects, then by paring them down to their logical essence, and cutting out all the distracting noise, it often becomes clearer what the nub of the problem is. So finding an answer to your question can become a lot easier.
The second advantage is power: if you have proved something about regular polyhedra, then what you have proved automatically holds true for every polyhedron, whether it's a cube, a tetrahedron, or some polyhedron that you have never even heard about.
All the ideas that mathematicians work with are arrived at by this process of abstraction, and none is more important than that of a group.
Groups: abstracting from addition
Let's think about all the whole numbers, or integers:
{... ,-3,-2,-1, 0, 1, 2, 3, ...}
together with the process of addition. You might notice three simple facts:
- if you add two integers together you get another integer;
- there is a special integer, 0, which does nothing when added to any other;
- from any integer, x say, you can get to 0 by adding its negative, -x.
- the combination of any two object is also an object in our set;
- there's one special object that when combined with any other object leaves the other object unchanged (let's call this special object 0);
- for every object in your set there always is another object, so that the combination of the two gets us back to 0.
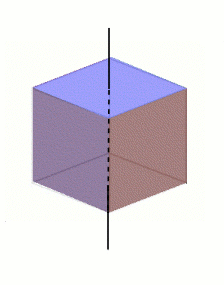
This axis passes through opposite faces of the cube. You can rotate it about this axis through 90, 180 and 270 degrees without changing its appearance. There are three different axes of this type, giving us a total of 9 rotations that leave the cube unchanged.
So, having abstracted from the integers and come up with the notion of a group, what other examples are there? It's no exaggeration to say that groups are everywhere in mathematics. They come in both finite and infinite varieties. The whole numbers discussed above give us an infinite group, because there are infinitely many of them. Of primary concern in this article though are the finite groups.
The cube can provide us with an example of a finite group: not the cube itself, but its collection of rotations. If I were to push a needle through the middle of the cube (through the centres either of two opposite faces, or of two opposite edges, or through two opposite vertices), then I could rotate the cube around this axis, so that some or all of the faces swap places. Unless you have labelled the faces, edges, or vertices, the cube will appear unchanged after such a rotation.
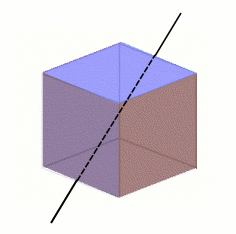
This axis passes through opposite edges of the cube. You can rotate it about this axis through 180 degrees without changing its appearance. There are six different axes of this type, giving us a total of 6 rotations that leave the cube unchanged.
The collection of all possible such rotations of the cube forms a group: if you perform one rotation and then a second, the combination is equivalent to performing a third (this is not immediately obvious); there is a rotation which does nothing at all (namely leaving the cube alone); and when you have performed any rotation you can get back to your starting position by doing your rotation backwards (or by rotating in the same direction so that the total angle of rotation amounts to 360 degrees).
It's not hard to see that there are 24 distinct rotations: 9 corresponding to having the axis through two opposite faces, 6 if the axis is through two edges, 8 if the axis is through two vertices, and the one trivial rotation which leaves it alone. These 24 rotations are called the elements of the group of rotations. Thus, the rotations of a cube form a finite group, in contrast to the group of whole numbers, which is infinite.
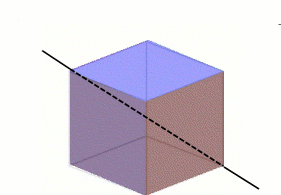
This axis passes through opposite vertices of the cube. You can rotate it about this axis through 120 and 240 degrees without changing its appearance. There are four different axes of this type, giving us a total of 8 rotations that leave the cube unchanged.
Of course we didn't have to start with a cube. For each regular polyhedron, there is a finite rotation group. In fact, mathematics is full of geometric structures, much more abstract than our regular polyhedra. Nonetheless, they often have automorphism groups associated to them, which relate to them (roughly speaking) in the same way as the group of rotations relates to the cube.
Classification: pinning down the abstract
If abstraction provides mathematicians with their objects of study, the theorems they try to prove often go the other way: from the general to the specific. They try to classify these abstract objects, that is to say to give a detailed and exhaustive list of all the objects which satisfy the definition.
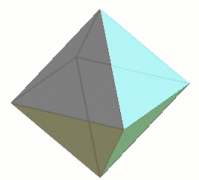
An octahedron has eight faces, each an equilateral triangle.
For example, having arrived at the notion of a regular polyhedron from the example of the cube, there is a corresponding classification theorem (which was known to the ancient Greeks). It states that every regular polyhedron, must be one of the Platonic solids: either a tetrahedron, a cube, an octahedron, a dodecahedron, or an icosahedron.
This is no longer just a list of examples, the fact that each of the Platonic solids is a regular polyhedron is only half the point. The other half is that there are no other regular polyhedra.
This is exactly the sort of theorem that researchers in many areas of mathematics would absolutely love to prove. So finite group theorists have achieved a truly enviable result. However, their classification doesn't apply to the class of all finite groups, just to one particularly important subclass.
Simple groups: algebra's atoms
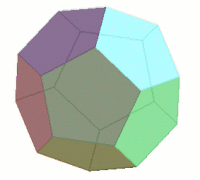
A dodecahedron has twelve faces, each being a regular pentagon.
The definition of a simple group is technical, but the idea is easy: just as a prime number is a number which cannot be factorised into two smaller numbers, so a group is simple if it cannot be broken up into two smaller groups.
As an example, let's go back to our cube and imagine that we've stuck a skewer through the mid-points of two opposite faces. We can rotate the cube around this axis by 90, 180, or 270 degrees without changing its appearance, and we can also leave it alone and do nothing. These four rotations, doing nothing and rotating through 90, 180 and 270 degrees, are four of the 24 elements of our rotation group.
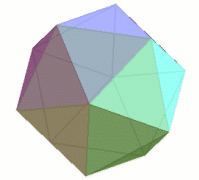
An icosahedron has twenty faces, each is an equilateral triangle.
However, they themselves also form a smaller group, as you can easily check. Doing two of these rotations in sequence, say first the 90 degree and then the 180 degree one, amounts to doing one of the other two, in this case the 270 degree one. There's the trivial rotation of doing nothing. And if you've done one rotation, say the 90 degree one, then following it by one of the other four, in this case the 270 degree rotation, gets you back to where you started. So these four rotations together satisfy our three characteristics that define a group.
Thus, the full group of rotations of a cube contains smaller groups that sit within it. Essentially, although the precise definition is more technical, a simple group is one that cannot be broken up into smaller groups in this way. Maybe one lesson to be learnt from the classification is that mathematicians should be more careful when naming things!
The importance of simple groups stems from the Jordan-Hölder Theorem, proved around 1889. It tells us that just as all molecules are built from atoms, and all positive integers are built from prime numbers, so all finite groups are built from finite simple groups. Once you understand the finite simple groups, you understand a lot about all finite groups.
The classification: anything but simple
Just as in the case of regular polyhedra, the classification of finite simple groups provides a complete list of all the finite simple groups. However there is a difference: this time the list is infinite; there are infinitely many distinct finite simple groups.
But despite their infinite number, mathematicians understand them well. There are precise descriptions of 18 infinite families of finite simple groups. The definitions are highly technical and delicate, but essentially they are obtained from families of automorphism groups of certain geometric structures. They are abstract analogues of the rotation groups of our regular polyhedra.
On top of these 18 families, there are 26 individual groups, the so-called sporadic groups. The largest of these is called the Monster and weighs in at 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 elements!
So now we understand what the classification of finite simple groups says: every finite simple group either belongs to one of the 18 families, or is one of the 26 sporadic groups.
After the classification: where now?
When the classification was announced, some people jumped to the conclusion that finite group theory had reached its end. But many mathematicians are still working in the area today. What are they doing?
One thing they're doing is simplifying the proof. Although the statement of the classification has already been very useful in a range of mathematical areas, a vast and impenetrable proof which no-one understands is of no use to anyone. There is a real risk that if the techniques get forgotten before the proof is put into an accessible form, then, in the words of Gorenstein, "it will gradually become lost to the living world of mathematics, buried deep within the dusty pages of forgotten journals".
So there are currently several projects afoot to consolidate and simplify parts of the proof. Perhaps the most significant was initiated by Gorenstein, along with Richard Lyons and Ronald Solomon, and is still ongoing: to produce a self-contained, slimmed down second generation proof, fully written down in one place. This is being done in a series of books being published by the American Mathematical Society. It is expected that they will number about twelve, and stretch to a total of 3,000-4,000 pages. At time of writing, 6 have been published so far.
A second major theme in finite group theory is the extension problem for finite groups. If simple groups are analogous to atoms, then it's worth noting that chemistry was far from finished when the Periodic Table was first published. Chemists wanted to understand the ways in which atoms could combine to form bigger molecules. So what are the equivalents of covalent and ionic bonds in the case of finite groups? What limits are there on the compound structures which can be built? A complete answer to this question would constitute a classification of all finite groups. But this isn't thought to be a viable goal at present. In full generality it seems inaccessibly hard. However various instances of the extension problem form the focus of much mathematical attention.
So much for finite groups. What about infinite groups? Is it feasible that something similar could be done there? Again, probably not in full generality: infinite groups come in a bewildering variety of forms. But this has led some mathematicians to look for tame subclasses of infinite groups, which might be amenable to this sort of analysis. Much of the current drive in this area rests on emulating the powerful techniques used in the classification of finite simple groups.
Let 'em roll
Dice are invaluable to many games, especially gambling games, but instead of playing with ordinary 1-6 numbered dice here are two interesting alternatives — with a twist!

Welcome to the Maths Casino!
Sicherman Dice
No doubt you are familiar with rolling a pair of dice and summing the spots — take Monopoly for example. But is there a different pair of dice that will still give a fair game? This was the problem conceived and solved by Colonel George Sicherman in the 1970s.
| + | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Sicherman aimed to find a different pair of six sided dice with positive integer face values, with the same probability distribution as a pair or ordinary dice. Having the same probability distribution ensures you still have the same chance of achieving a certain score.
| Possible scores | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Probability that you will roll that score | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
There is one such pair of dice — Die 1 with faces 1, 2, 2, 3, 3, 4 and die 2 with faces 1, 3, 4, 5, 6, 8 — but how did Sicherman find it?

Sicherman Dice
The answer lies in expressing a die as a polynomial. (A polynomial is an expression with terms involving a variable, x, raised to different integer powers). For each term in the polynomial, the power of x represents the face value and the coefficient the number of faces with that value.
An ordinary die would therefore be expressed:
|
|
|
The polynomial obtained is in fact an expression of the probability distribution of rolling two dice. It is easy to see that if a term nxc appears in the product (B), then there are exactly n combinations of rolls that give you the sum c, and vice versa. (Out of the 36 possible rolls, there are one 12, two 11's, three 10's, four 9's, five 8's, six 7's, five 6's, three 4's, two 3's, and one 2.) So multiplying the polynmoials corresponds to considering the sum of two rolls.
To find the Sicherman Dice an alternative pair of factors for (B) must be generated. So we need to consider the following constraints:
- Faces cannot be blank so the generated pairs cannot have x0 terms (x0 = 1) .
- The dice have six faces so the coefficients must add to six.
(This can be checked by setting x = 1 and as 1n = 1 the answer should be 6.) - All factors of (B) must be included in the alternative pair of factors.
To begin factorising (B), let us first consider factorising (A) and then simply square our answer:
|
Therefore factors of (B), ( x6 + x5 + x4 + x3 + x2 + x )2, are:
|
Valid pairs of dice can now be found by splitting (C) into pairs of polynomials. In (C) we have two x factors, two (x2 + x + 1) factors, two (x2 - x + 1) factors, and two (x + 1) factors. And we can use any combination of these that obeys the constraints.
To get no x0 terms, both of the polynomials in the pair must contain one of the x factors. (Otherwise we will be left with "1" from multiplying out the other brackets.)
To ensure we have each die with six faces, both of the polynmoials must equal 6 when x = 1. And to have this value of 6 each polynmoial must contain a factor equal to 3, and a factor equal to 2 when x = 1. This corresponds to both of the polynomials having an (x2 + x + 1) and an (x + 1) factor.
In fact these constraints only leave the two (x2 - x + 1) factors to play with! There are two potential combinations:
Combination A:
Die 1: x (x2 + x + 1)(x + 1)(x2 - x + 1)
Die 2: x (x2 + x + 1)(x + 1)(x2 - x + 1)
When multiplied out these are the ordinary dice.
Combination B:
Die 1: x (x2 + x + 1)(x + 1)
Die 2: x (x2 + x + 1)(x + 1)(x2 - x + 1)2
And multiplying these out we get the polynomials for the Sicherman Dice:
Die 1: x4 + 2x3 + 2x2 + x
Die 2: x8 + x6 + x5 + x4 + x3 + x
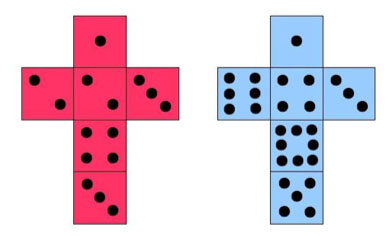
Nets of Sicherman's Dice
| + | 1 | 2 | 2 | 3 | 3 | 4 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 3 | 4 | 4 | 5 |
| 3 | 4 | 5 | 5 | 6 | 6 | 7 |
| 4 | 5 | 6 | 6 | 7 | 7 | 8 |
| 5 | 6 | 7 | 7 | 8 | 8 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 10 |
| 8 | 9 | 10 | 10 | 11 | 11 | 12 |
An interesting point to note is that sums of the opposite sides are 5 and 9 respectively which averages to 7, the sum of the opposite sides on a normal die.
And, as sought, our probability distribution is the same as for a pair of ordinary dice.
| Possible scores | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Probability that you will roll that score | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
By changing the constraints similar sets of dice can be investigated using the same method. If blank sides are allowed we can play around with the x factor to find two other pairs of Sicherman-like dice.
And the dice need not be six sided, any platonic solid may be used. (Arguably any solids at all could be used, but many would have an irregular weight distribution and be biased dice.) Generally as the number of faces on the die and terms in the polynomial increases there are more viable pairs of dice. For example, an octahedron has three combinations and a dodecahedron thirteen. However this is not always the case, a 35 sided shape again has only one pair!
You might like to take the problem one stage further:
- Could the same method be used for triplets of dice?
- By starting with any probability distribution and expressing it as a polynomial could dice then be found to give that distribution?
 paper and paper beats rock, but
paper and paper beats rock, but scissors are no match for rock" height="291" width="200">
A non-transitive game: scissors beat
paper and paper beats rock, but
scissors are no match for rock
Efron's Dice
Now we play a different game with another set of unusual dice. They were invented by Bradley Efron, a statistician at Stanford University, California.
The game now consists of two players picking one of three dice and rolling it, with the highest score winning. Efron's Dice have interesting probability properties. They are non-transitive. This means that although die A beats die B, and die beats die C, die C beats die A! This is somewhat counterintuitive but think of the playground game "Rock, Paper, Scissors", perhaps a more familiar non-transitive situation.
But what are the dice?
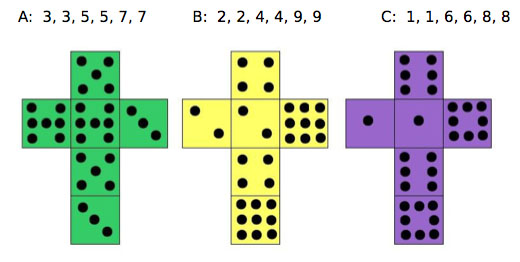
Nets of Efron's Dice
Looking at a wins/losses table, the non-transitive nature of these dice can easily be seen:
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In fact the probability of A beating B, B beating C, and C beating A is always 20/36 = 5/9.
Therefore the winning strategy is simple: let your opponent pick their dice first then pick its superior. For example if they choose A, you choose C.
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
It is interesting to note that arranging the values of these dice can make a magic square. The three values of each die are all placed in the same row or column and when correctly arranged the rows, columns and diagonals will all have a total of fifteen.
Efron also designed three sets of four die which are also non-transitive.
|
|
| ||||||||||||||||||||||||||||||
Again the wins/losses tables can be used to verify this and find the probability of winning. For Set 1:
P(A>B) = P(B>C) = P(C>D) = P(D>A) = 2/3
where P(A>B) means the probability of A beating B.
Of course, now we have 4 dice there are other combinations which are not covered in the above combinations. We could also trying playing A against C, or B against D.
| Using Set 1 again: | P(A>C) = 4/9 |
| P(B>D) = 1/2 (the same as ordinary dice) |
Okay, so using Efron's Dice , to have the upper hand your opponent must choose first. However what if you have to choose first? Fascinatingly, with a set of three dice found by Allen Schwenk, from Western Michigan University, if you change the rules of the game slightly the probability switches and you again have the advantage.
Schwenk's Dice
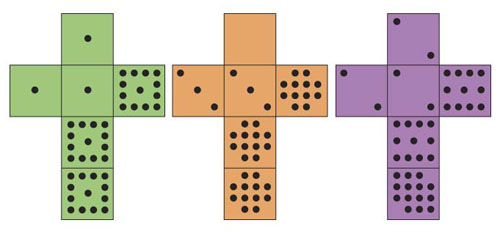
Nets of Schwenk's dice
| A: 1, 1, 1, 13, 13, 13 | B: 0, 3, 3, 12, 12, 12 | C: 2, 2, 2, 11, 11, 14 |
Firstly considering Schwenk's Dice normally with one roll, you can calculate the wins/losses tables to see that:
P(A>B) = P(B>C) = P(C>A) = 7/12
So in the game if you have had to pick first, say you picked die B, a clever opponent might pick die A, as this has an advantage over your die when playing with just one roll. But you can still turn the tables by changing the rules of the game: now you and your opponent compete with the total of two rolls (both with your chosen die).
To find your winning chances with the total of two rolls we must find the probability distribution for each dice and its possible totals.
| Die A | ||||||
|---|---|---|---|---|---|---|
| + | 1 | 1 | 1 | 13 | 13 | 13 |
| 1 | 2 | 2 | 2 | 14 | 14 | 14 |
| 1 | 2 | 2 | 2 | 14 | 14 | 14 |
| 1 | 2 | 2 | 2 | 14 | 14 | 14 |
| 13 | 14 | 14 | 14 | 26 | 26 | 26 |
| 13 | 14 | 14 | 14 | 26 | 26 | 26 |
| 13 | 14 | 14 | 14 | 26 | 26 | 26 |
The possible totals for two rolls of Die A of Schwenk's Dice, and the probability table for those scores.
| a | 2 | 14 | 26 |
|---|---|---|---|
| P(A=a) | 1/4 | 1/2 | 1/4 |
| Die B | ||||||
|---|---|---|---|---|---|---|
| + | 0 | 3 | 3 | 12 | 12 | 12 |
| 0 | 0 | 3 | 3 | 12 | 12 | 12 |
| 3 | 3 | 6 | 6 | 15 | 15 | 15 |
| 3 | 3 | 6 | 6 | 15 | 15 | 15 |
| 12 | 12 | 15 | 15 | 24 | 24 | 24 |
| 12 | 12 | 15 | 15 | 24 | 24 | 24 |
| 12 | 12 | 15 | 15 | 24 | 24 | 24 |
The possible totals for two rolls of Die B of Schwenk's Dice, and the probability table for those scores.
| b | 0 | 3 | 6 | 12 | 15 | 24 |
|---|---|---|---|---|---|---|
| P(B=b) | 1/36 | 1/9 | 1/9 | 1/6 | 1/3 | 1/4 |
| Die C | ||||||
|---|---|---|---|---|---|---|
| + | 2 | 2 | 2 | 11 | 11 | 14 |
| 2 | 4 | 4 | 4 | 13 | 13 | 16 |
| 2 | 4 | 4 | 4 | 13 | 13 | 16 |
| 2 | 4 | 4 | 4 | 13 | 13 | 16 |
| 11 | 13 | 13 | 13 | 22 | 22 | 25 |
| 11 | 13 | 13 | 13 | 22 | 22 | 25 |
| 14 | 16 | 16 | 16 | 25 | 25 | 28 |
The possible totals for two rolls of Die C of Schwenk's Dice, and the probability table for those scores.
| c | 4 | 13 | 16 | 22 | 25 | 28 |
|---|---|---|---|---|---|---|
| P(C=c) | 1/4 | 1/3 | 1/6 | 1/9 | 1/9 | 1/36 |
The wins/losses tables for the game (competing with a total of two rolls) are again constructed with these possible totals. For example, the game of die A against die B is won or lost as follows:
| Die A | ||||
|---|---|---|---|---|
| D i e B | 2 | 14 | 26 | |
| 0 | W | W | W | |
| 3 | L | W | W | |
| 6 | L | W | W | |
| 12 | L | W | W | |
| 15 | L | L | W | |
| 24 | L | L | W | |
However care must be taken interpreting this table as the probability of achieving the values for die A and B are no longer equal. The probability of die A winning therefore is not the easy answer of 11/18, but is instead the sum of the different probabilities for each win.
We write each winning combination in the form P(a,b) (where a and b are a possible value of dice A and B respectively).
P(2,0) = P(A=2) x P(B=0) = 1/4 x 1/36 = 1/144
P(14,0) = P(A=14) x P(B=0) = 1/2 x 1/36 = 1/72
P(26,0) = P(A=26) x P(B=0) = 1/4 x 1/36 = 1/144
P(14,3) = P(A=14) x P(B=3) = 1/2 x 1/9 = 1/18 ...
When the probabilities of all the winning combinations are summed P(A>B) is produced, and as expected, B now does have marginally better chances of beating A. By using the same technique (you do get quite quick at it) the probabilities of C now beating B and A beating C can be established.
So both Efron's and Schwenk's dice give you an advantage when your opponents has to pick their die first. But only Schwenk's dice, along with a little tweaking of the game, gives you an advantage if you have to take first pick. But what would happen if you changed the rules and rolled Efron's Dice twice? And, with Schwenk's dice, who will have the advantage with three rolls, or four, or, for the very brave, n rolls?
These are just a few examples of mathematics in the gaming world, and there are many other dice and dicing games in existence with interesting irregularities, try a little internet browsing! Undoubtedly there are also plenty yet to be designed which, as these dice demonstrate, only requires some basic mathematics. Therefore finding them is potentially an open opportunity for all, as it just requires an imaginative mind and some spare time.
Math Animations Illustrate Research, Herald New Era In Visualization
The two collaborators are Etienne Ghys, a mathematician at the Ecole Normale Sup'rieure in Lyon, France, and Jos Leys, a Belgian graphic artist and engineer with strong mathematical interests. They have written an online animated exposition of an important new theorem Ghys has proved in dynamical systems theory. The exposition will appear as the November 2006 installment of the Feature Column on the web site of the American Mathematical Society.
 The two collaborators are Etienne Ghys, a mathematician at the Ecole Normale Sup´rieure in Lyon, France, and Jos Leys, a Belgian graphic artist and engineer with strong mathematical interests. They have written an online animated exposition of an important new theorem Ghys has proved in dynamical systems theory. The exposition will appear as the November 2006 installment of the Feature Column on the web site of the American Mathematical Society.
The two collaborators are Etienne Ghys, a mathematician at the Ecole Normale Sup´rieure in Lyon, France, and Jos Leys, a Belgian graphic artist and engineer with strong mathematical interests. They have written an online animated exposition of an important new theorem Ghys has proved in dynamical systems theory. The exposition will appear as the November 2006 installment of the Feature Column on the web site of the American Mathematical Society.Ghys's Theorem: A Deep Connection in Dynamical Systems Theory
Ghys was preparing a lecture for the Bibliothèque National de France when he found some intriguing mathematical pictures on Leys's web site. Soon the two were discussing making illustrations of a theorem that Ghys had recently proved, which gives a deep connection between two seemingly unrelated phenomena in dynamical systems theory: Lorenz attractors and modular flows. A dynamical system is a system that evolves over time, like the weather or the stock market. Mathematicians study the differential equations that describe how dynamical systems change over time.
Lorenz attractors: The Lorenz attractor has become the paradigmatic image of chaos theory. In the 1960s the meteorologist Edward Lorenz stumbled on this "strange attractor" in his research examining a particular dynamical system that modeled weather patterns. As that system evolves, the points in it trace out trajectories that return back to their original locations, forming periodic orbits that accumulate around the attractor (hence the name). The orbits are knots: closed loops in 3-dimensional space. Out of the infinite universe of mathematical knots, only a small set of very special knots appear in the Lorenz attractor. The animations of Ghys and Leys display these special Lorenz knots and show how the knots determine the shape of the Lorenz attractor.
Modular flows: A lattice is a collection of evenly-spaced points in the plane, like the set of dots in the Dots and Boxes game. A dynamical system, or flow, on the lattice is a rule for making the lattice points move in a uniform way across the plane. This notion of "modular flow" has been an important tool in mathematics, in particular in number theory, where its roots go back to the great German mathematician Carl Friedrich Gauss (1777-1855). Ghys showed how each modular flow can be associated in a unique way with a knot---and he discovered that the set of knots associated with modular flows is exactly the set of Lorenz knots!
This extraordinary result, and the animations illustrating it, formed the centerpiece for a plenary lecture Ghys presented at the quadrennial International Congress of Mathematicians in Madrid, Spain, in August 2006. Being invited to present an ICM plenary lecture is a coveted honor in the mathematical world. Ghys's lecture was enthusiastically received and constituted a major highlight of the Congress, which was attended by 4000 mathematicians from all over the world.
Getting the Knots to Close
When Ghys and Leys first began working together, they intended to produce still images to illustrate Ghys's theorem. "Soon, we realized that animations are much more fun than still images," Ghys said. The two worked closely to develop numerical algorithms to carry out the animations. All of the work was done on their personal computers, and their interaction has been almost entirely through email. "It was an intense collaboration," said Leys. "We exchanged about 1,800 email messages in 4 months, a lot of them sent late at night when we were close to a breakthrough." While Leys wrote code in a program called UltraFractal that is good for pictures but not ideal for mathematics, Ghys would work in parallel using specialized mathematical software packages to provide hints about how the computations should be done.
The perfection with which the animations capture the mathematical world of dynamical systems and knots came as a result of hard work---and a great deal of back and forth between Ghys and Leys. "Almost never did our knots close!" Ghys recalled. "Most of the time, the knots came out in several pieces not connected together." The errors were caused sometimes by wrong formulae, and sometimes because of numerical artifacts arising from the computing scheme. As Ghys and Leys worked together to find the best way to represent the mathematics, each learned about the other's area of expertise.
Their animations offer a glimpse deep into the heart of a mathematical world that few have been able to see until now. By the time they had begun collaborating, Ghys already had a mathematical proof of his theorem. But the animations brought him to a new level of understanding. "When I saw the proof in action, I was 'more convinced' that it is true!"
Link to the Riemann Hypothesis
At the end of their Feature Column, Ghys and Leys present an animation of yet another kind of dynamical system called a horocycle flow. There is a link between this flow and a question known as the Riemann Hypothesis, which is a statement about the distribution of prime numbers and is perhaps the biggest open problem in mathematics today. If one could prove a certain fact about the horocycle flow, the Riemann Hypothesis would follow as a consequence.
Sunday, January 21, 2007
Election Results Continue To Puzzle
After the Election Commission reviewed the votes Wednesday, the turnout jumped from 49 percent to 83 percent. That catapulted Benton County to the top of the turnout heap, according to totals from Secretary of State's Web site on Friday. The county with the second-highest turnout was Madison County with 64 percent.
The observance of Veterans Day on Friday made it impossible to get many answers from county officials.
Robbyn Tumey, former chairwoman of the Benton County Democratic Party, went to the Election Commission office on Friday to speak with Jim McCarthy, election coordinator. Tumey worked on the media plan for Cheryl Murphy, District 2 justice of the peace candidate. Revised results released Thursday showed Murphy had lost her race to Republican Frank Winscott. Tuesday's results first showed she was winning and later showed she would face a runoff with Winscott.
Tumey said she is prepared to file an injunction to stop the Election Commission from certifying the election. She said she and McCarthy looked over the results together. Some, such as a Rogers precinct with more than 100 percent voter turnout, alarmed both of them. He then gathered the voting system's computer disks and flash drives and told her he was headed to the Election Systems & Software office in Little Rock, she said.
Election Systems & Software has a statewide contract to provide voting machines.
Calls to Jim McCarthy's cell phone went straight to voicemail, which was full. An employee who answered the telephone at the Election Systems & Software office in Little Rock said he could not speak to the media. Election Systems & Software media representatives in Omaha, Neb., where the company is based, said they were not aware of the situation and could not comment.
Murphy said the unprecedented turnout caused her and some others to question the latest election results.
In her district alone, a 92 percent turnout was recorded, she said. That just doesn't happen in District 2, which is rural, divided by Beaver Lake and generally has a lower turnout, she said.
"So to jump to an 80 percent turnout, I question," she said. "I heavily question."
A close analysis of Thursday's results show in two races, more people voted in a mayoral race than live in the town, according to the U.S. Census Bureau's July 2005 estimates. In Gateway, a town of 122 people, 199 votes were cast in an uncontested mayoral race. In the Pea Ridge, 3,997 votes were cast in a contested mayor's race for the city of 3,344 people.
Lynn Chinn, Democratic election commissioner, said he was not able to reach McCarthy on Friday and had not heard of the latest apparent problems with the election results.
A turnout of more than 80 percent is exceptional even for a hotly contest presidential election, said Andrew Dowdle, assistant professor of political science at University of Arkansas. He pointed out Idaho made news this week with 63 percent voter turnout in a midterm election.
"An understatement is that (83 percent) is a little high in terms of a midterm election," said Dowdle, who specializes in elections and campaigns. "Eighty-three percent is mathematically possible, but again, just something that would be kind of an eye-popping figure."
The commission decided to review the election results after noticing problems, such as precincts with unusually low turnout.
The commission announced the results of its review of results Thursday afternoon, after working until 3 a.m. that morning to fix a computer problem that threw out tabulated votes as new votes were entered on election night. McCarthy said Thursday the Election Commission's attempt to share real-time results with partygoers at the Clarion Hotel in Bentonville caused the glitch.
The retabulated results changed the outcome of eight contests, mostly in tight races or races with few votes cast.
The revised Thursday report said 79,331 of 95,900 registered voters, or 83 percent, cast ballots. The original results released on election night said 47,134 voters, or 49 percent, cast ballots.
PocketCru is a crossword puzzle maker for Pocket PC
PocketCru can also be used with a clue database to select clues for the grid. You can also write your own clues.
To use PocketCru, you will need a Pocket PC and a word list. You will need lots of free program memory. You can also optionally use a clue database. If your word list or clue database is large, then you will need a memory card to store those items.
PocketCru can be downloaded here: PocketCru. PocketCru does NOT have a setup program. To install PocketCru, you need to use the Explore feature of ActiveSync. Copy PocketCru.exe to your device. If you want it on the start menu, copy it to \Windows\Start Menu. If you want it in your Programs listing, then copy it to \Windows\Start Menu\Programs.
If you use Crossword Compiler by Anthony Lewis, you can use your favorite word lists by doing these steps:
* 1. Start Crossword Compiler.
* 2. Under the Words menu, go to Word List Manager.
* 3. Select the word list you want to use.
* 4. Under the Convert menu, go to List to plain text or theme list.
* 5. Save the file.
* 6. When it asks if you want to include word scores, say Yes.
* 7. Copy the file to your Pocket PC. It needs to be in a place where Pocket PC programs can open it, usually under My Documents.
If you don't use Crossword Compiler, then just make your list one word on a line, followed by a semicolon, then the word score. It needs to have and extension of .txt. For instance:
AARDVARK;50
AARON;40
If you use Crossword Compiler by Anthony Lewis, you can use your favorite clue database by doing these steps:
* 1. Start Crossword Compiler
* 2. Under the Clue menu, go to Database manager
* 3. Select the clue database you want to use
* 4. Under the Menu button dropdown, go to Tidy file. Tidying the file puts it in alphabetical order, which PocketCru requires.
* 5. Go to your clue database directory (usually C:\Program Files\Crossword Compiler 7\Clue Databases)
* 6. Copy the clue database to your Pocket PC. The one you need to copy will end in .csv. It needs to be in a place where Pocket PC programs can open it, usually under My Documents.
If you don't use Crossword Compiler, then just put the word, followed by a comma, then the clue, then a comma, then a date. It needs to have and extension of .csv. It needs to follow standard rules about commas and quote marks in comma separated value files. For instance:
aaa,"Motel approver, briefly",2006-01-19
aaa,"Towers, at times: Abbr.",2006-01-19
aaa,Baseball club designation,2006-01-19
aaa,Battery buy,2006-01-18
aaa,Battery designation,2006-01-19
Basic Interface
* Tap on a white square to move the selection.
* Tap on the selected square to change direction. Yellow is across, light blue is down.
* Double-tap on a square to change it to a block.
* Double-tap on a block to change it back to a white square.
* Use the letters at the bottom of the screen to enter letters into the grid. The "Sp" at the right will insert a space. The "Tg" will toggle the direction.
Manual Fill
Manual Set Clues
21x21 Grid
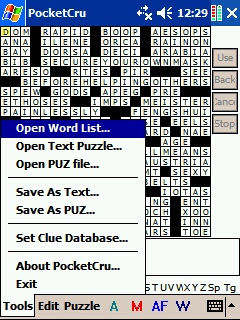
Tools Menu
* Open Word List - Opens a word list. Must be done before filling the grid or using the Find Word dialog. This step requires a lot of program memory.
* Open Text Puzzle - Opens a puzzle exported to text from Crossword Compiler.
* Open PUZ file - Opens an Across Lite format puzzle.
* Save As Text - Saves a puzzle to text format. You can open this file in Crossword Compiler by changing the type of files to open to Text files.
* Save As PUZ - Saves to Across Lite format. The puzzle can then be read by any program that reads Across Lite puzzles, except Across Lite (because they use some data in the file header for file format protection)
* Set Clue Database - Sets the clue database to use when filling the grid and setting clues. The clue database is NOT read to memory, so you can use large clue databases.
* About PocketCru - Brings up the about box.
* Exit - Exit the program.
Edit Menu
* Clear Word - Clears all letters from the current word. If the selected square is yellow, then it will remove the across word. If the selected square is blue, it will remove the down word.
* Clear All Letters - Clears all letters from the puzzle.
* Remove Blocks - Removes all blocks.
Puzzle Menu
* Autofind - Finds all words that fit the current selection. If the selected square is yellow, then it will use the across word. If the selected square is blue, it will use the down word.
* Find Word - Opens the Find Word dialog.
* Auto Fill - Fills the grid without user interaction.
* Manual Fill - Fills the grid by allowing the user to select each word. The words it suggests are listed in recommended order.
* Auto Set Clues - After filling the grid, use this option to automatically set clues to words. This option will overwrite any clues you have already set.
* Manual Set Clues - Manually set clues one at a time. It will start at the currently selected word. You can choose a clue from the clue database, or type in a new clue (above the grid).
* Check Crossers - When using Autofind, if this option is checked it will only show words that have potential crossers.
* Use Optimization - Use this option for a faster auto fill. It also adds a bit of random selection to auto fill. You can use this option in manual fill, but it is not recommended.
* Show Clues During Fill - Shows clues in a combobox above the grid during manual fill.
* Next Word Linked - If checked, it requires the program to require the program to move to a linked word during auto or manual fill, if possible.
* Start at Current Word - Begins the auto fill or manual fill from the currently selected location.
Find Word dialog
* Find - Click the find button to find words that match the pattern in the edit box. If you type *, it will match 0 or more characters at that position. If you type an alphabetic character, it will match the character. If you type any other character (such as ? or .), it will match exactly one character at that position.
* Minimum Length - Sets the minimum number of characters in the found words.
* Maximum Length - Sets the maximum number of characters in the found words.
* By Length? - If checked, then the word list will be sorted by length.
* Maximum Words Found - Sets the maximum number of words to find to match the pattern.
If you select a word, it will show clues for that word.